సరళ హరాత్మక డోలనము

సరళ హరాత్మక డోలకము

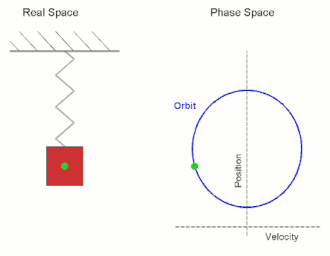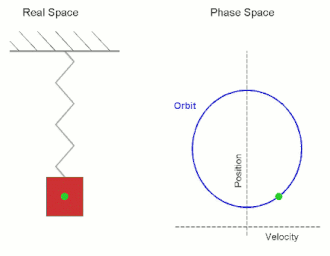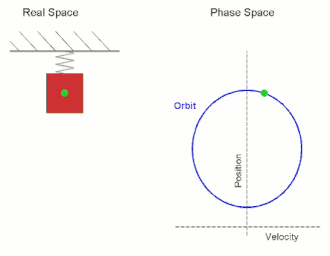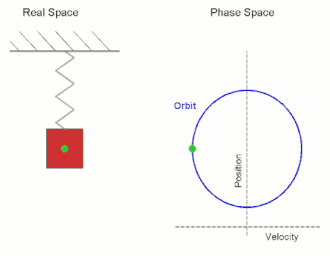
స్ర్పింగు ఒక కొనకు తగి లించిన వస్తువు ఒక దానిని పటం లో చూడవచ్చు. స్ర్పింగు రెండో కొన గట్టి ఆధారానికి కట్టి ఉంది. వస్తువు క్షితిజ సమాంతరవు ఫలకం మీద స్పేచ్చగా కదలడానికి వీలుగా ఏర్పాట్లు చేసినామను కొందాము. స్ర్పింగు చాలా తేలిక అవటం వల్ల దాని ద్రవ్యరాశిని లెక్క చేయనవసరంలేదు. 'm' ద్రవ్యరాశిగల వస్తువును కొద్దిగా లాగితే స్ర్పింగు సాగుతుంది. స్ర్పింగును సాగదీయడానికి కావలసిన బలము వ్యావనానికి (extension) అనులోమానుపాతంలో ఉంటుంది. వస్తువును నిశ్చలస్థానం నుంచి కుడి వైపు 'x' దూరం లాగి వదలినామనుకొందాము. అప్పుడు స్ర్పింగు తన వూర్వ స్దితికి రావడానికి ప్రయోగించే పునఃస్థాపక బలము (restoring force) వస్తువును దాని పూర్వ స్థానానికి లాగుతుంది. ఈ బలము 'x' కు అనులోమాను పాతంలో ఉండి వ్యతిరేక దిశలో వనిచేస్తుంది.

$\overrightarrow{F}=-k\overrightarrow{x}$-----------------1

ఇక్కడ k అనేది ధన స్థిరాంకము

సరళ హరాత్మక చలనము

సరళ హరాత్మక చలము

న్యూటన్ రెండో గమన సూత్రం ప్రకారం పునఃస్థాపక బలము,

$F=ma=m\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}=-kx.$ ------------2

F కు ఈ విలువను పై 1 సమీకరణంలో ప్రతి క్షేపి స్తే

$F_{net}=m\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}=-kx,$-----------3

అవుతుంది. ఇది ద్విఘాత అవకలన సమీకరణమ సరళ హరాత్మక డోలనపు చలనాన్ని వూర్తిగా నిర్వచిస్తుంది. ఏ క్షణంలో నైనా వస్తువు ఉనికి తెలుసుకోవాలంటే ఈ సమీకరణాన్ని సాధించాలి.

$F_{net}=m\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}=-kx,$----------4

ఈ సమీకరణంలో x, tయొక్క ప్రమేయంగా ఉంది. అవకలన గణితం (differental calculus) ప్రకారం ఈ ధర్మము సైన్ ప్రమేయాలకు ఉంటుంది. స్ధిరాంకంతో కోసై న్ను పెంచినా, tకి ఒక స్ధిరాంకాన్ని కలిపినా ఈ ధర్మం మారదు.

$x(t)=c_1\cos \left(\omega t\right)+c_2\sin \left(\omega t\right)=A\cos (\omega t-\phi ),$--------5

అనుకొందాము. ఇందులోA, ω, φలు స్థిరాంకాలు. వీటి చ్విలువలు తెలుస్ల్కొగలిగితే స్మీకరణానికి పూర్తి పరిష్కారం లభించిన్నట్లే. వీటి విలువను కనుక్కోవడానికి x విలువను 5వ సమీకరణములో ప్రతిక్షేపిద్దాము.

$v(t)=\frac{\mathrm{d}x}{\mathrm{d}t}=-A\omega \sin (\omega t-\phi ),$

$a(t)=\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}=-A{\omega }^2\cos (\omega t-\phi ).$

ఈ విలువను 5వ సమీకరణఒలో ప్రతిక్షేపిస్తే

${\omega }^2=\sqrt{\frac{k}{m}},$అయినప్పుడు:$x(t)=A\cos (\omega t-\phi ),$అన్నది సరళ హరాత్మక డోలకపు చలన సమీకరణానికి పూర్తి పరిష్కారమవుతుంది. అప్పుడు

$\omega =\sqrt{\frac{k}{m}},$

A, φస్థిరాంకాల విలువలు తెలియవు. A, φల విలువలు ఎట్లాంటివయినా 5వ సమీకరణాన్ని త్రుప్తిపరుస్తాయి. అంటే ప్రస్తావించిన డోలకానికి అనేక రకాల చలనాలుండవచ్చు. :$\omega =\sqrt{\frac{k}{m}},$, కబట్టి, :$T=2\pi \sqrt{\frac{m}{k}}.$---------6 అంటే 5వ సమీకరణంతొస్ నిర్వచించిన హరాత్మక చలనాలన్నింటికి ఒకే అవర్తన కాలముంటుంది. అది k, mల మీద మాత్రమే ఆధారపడి ఉంటుంది. డోలకపు పౌనఃపున్యము:$f=\frac{1}{2\pi }\sqrt{\frac{k}{m}},$-------7

ఇవి కూడా చూడండి

• అవరుద్ధ హరాత్మక డోలకము
• ద్రవ్యరాశి

బయటి లంకెలు

• harmonicమూస:Dead link
• Chaosమూస:Dead link